Rational Numbers
Commutative And Associative Properties Of Rational Numbers
Consider the expression

What will be the value of this expression?
If we try to find the value of this expression by usually adding the terms in the bracket first and then by adding the result so obtained to the third term, then it will take a long time. Therefore here, we can make use of commutative and associative properties of addition of rational numbers to make our calculation simpler.
Let us first study these properties for rational numbers and then we will find the value of the above expression.
The commutative property of rational numbers over addition can be stated as follows.
“If a and b are any two rational numbers, then a + b = b + a”.
|
For example, consider the rational numbers 5/14 and -7/12.


∴ 

Here, the numbers 5/14 and -7/12 are arbitrary, therefore we can say that rational numbers are commutative under addition.
The associative property of rational numbers over addition can be stated as follows.
“If a, b, and c are any three rational numbers, then a + (b + c) = (a + b) + c”.
|
For example: consider the rational numbers

Let us first find the value of the expressions



∴ We have 

Here, the numbers 1/2, -2/3 and 1/3 are arbitrary, therefore we can say that rational numbers
are associative under addition.
Now, let us go back to our previous problem with which we started our discussion.
We can write (5/18+77/25) + -5/18 = (77/25+5/18) + -5/18 (using commutative property)

Thus, in this way, we can make use of commutative and associative properties of rational numbers to make our calculations easier and simpler.
Let us know about commutative and associative properties of rational numbers for other operations such as multiplication, division etc.
Rational numbers are commutative and associative under multiplication also.
We can write these properties for multiplication as follows.
If a, b and c are any three rational numbers, then
(i) a × b = b × a (commutative property)
(ii) a × (b × c) = (a × b) × c (associative property)
|
Rational numbers are not commutative and associative under subtraction.
For this, let us see the following example.
Consider the rational numbers 4/7 and 5/7

Therefore, we see that 

Thus, rational numbers are not commutative under subtraction.
In the same way, we can check that rational numbers are not associative under subtraction.
Now, let us check whether rational numbers are commutative and associative under division.
Let us find the value of




Thus, we find that rational numbers are not commutative under division.
To check associative property, let us consider three rational numbers 1/2, 1/4 and -1/5

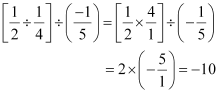

Thus, we can say that rational numbers are not associative under division.
We can summarize the above facts as follows.
|
Let us now look at some more examples.
Example 1:
Fill in the blanks using commutative and associative properties of rational numbers.
i.

ii.

iii.

iv.

Solution:
i. Rational numbers are commutative under addition.

ii. Rational numbers are commutative under multiplication.

iii. Rational numbers are associative under addition.

iv. Rational numbers are associative under multiplication.

Example 2:
Find the value of the following expressions using properties of rational numbers.
i.

ii.

Solution:
i.


ii.


